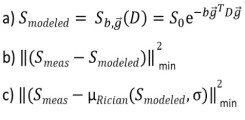Rician noise bias correction in Diffusion-Tensor- and Kurtosis- Imaging
Diffusion-Tensor and Kurtosis Imaging (DTI and DKI) parameters have been linked to biophysical properties of white matter such as fiber dispersion or axonal-water fraction (Fieremans et al., 2011; Edwards et al., 2017; Jespersen et al., 2018).
MRI magnitude images are formed by recording the MRI signal with a set of orthogonal receiver coils (the individual coils are called "In phase" and "Quadrature") and computing the magnitude, i.e. summing the square of the individually recorded signals and taking the root. Figure 1 symbolically shows MRI signal detection from the same precessing magnetization in a sample volume with such a set of receiver coils.
Using an incorrect Gaussian noise model introduces a bias into the estimated parameter maps (Polzehl and Tabelow, 2016), and, in turn, biases in the biophysical white matter parameters of interest.
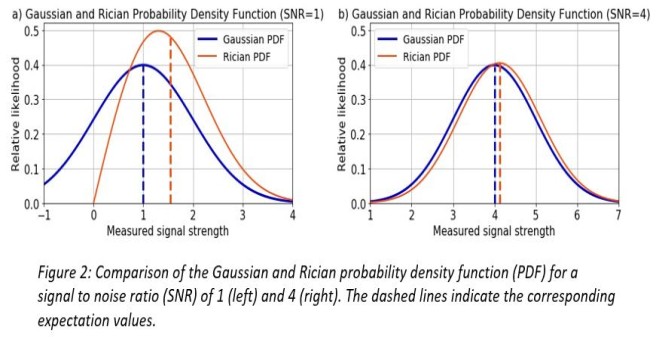
The severity of the bias is correlated to the signal-to-noise ratio (SNR). Figure 2 shows a comparison between the Gaussian and Rician probability density function (PDF) for an SNR of 1 and 4. A signal contaminated with Gaussian noise is modelled with the Gaussian expectation value (dashed vertical blue lines), a signal contaminated with Rician noise is modelled with the Rician expectation value (dashed vertical red lines). The difference between the Gaussian and Rician expectation value introduces a bias when doing parameter estimation assuming Gaussian noise.
The lower the SNR the greater the bias and vice versa (figure 2 a) and b)). Therefore, especially in the case of a low SNR, using the correct noise model for the MRI signal prediction in magnitude images is crucial to avoiding a bias in parameter estimation.
Central formulas for doing parameter estimation in DTI, here Smeas is the measured signal: a) noise-free DTI signal model, b) biased least square objective function assuming Gaussian noise, c) Rician noise corrected least square objective function using the Rician expectation value as a signal model. Parameter estimation e.g. in DTI is based upon the signal model a) predicting a noise-free signal depending on the b-value, direction of the diffusion gradient and the Diffusion-Tensor. The expectation value of a noise-free signal contaminated with Gaussian noise (dashed vertical blue line in figure 2) is the same as the noise-free signal itself because of symmetry of the Gaussian distribution. Parameter estimation in a non-linear least squares formalism is usually done by minimizing the objective function b) assuming Gaussian noise and is, therefore, biased. Rician noise corrected parameter estimation assumes the measured, noise contaminated signal to follow a Rician distribution and can be done by minimizing the objective function c) where the Rician expectation value (dashed vertical red line in figure 2) as a function of the signal model a) and a noise level sigma is used to model the measured data.
This Master-Thesis aim is to estimate DTI and DKI parameter maps using the correct noise model (i.e. Rician noise distribution) for diffusion weighted magnitude images. To this end, a nonlinear least squares fitting algorithm is implemented which uses the Rician expectation value as a signal prediction for the measured diffusion weighted MRI signal to find the optimal tensor parameters. These Rician noise corrected DTI and DKI parameters can then, finally, be utilized to compute biophysical parameters such as the axonal water fraction or fiber dispersion.
As a side project, the newly developed tools will be implemented into the ACID toolbox .
Acknowledgments:
This project is co-supervised by Dr. Karsten Tabelow at the Weierstrass Institute for Applied Analysis and Stochastics in Berlin and Prof. Dr. Florian Grüner at the Institute of Experimental Physics at the University of Hamburg.
References
Edwards LJ, Pine KJ, Ellerbrock I, Weiskopf N, Mohammadi S (2017) NODDI-DTI: Estimating Neurite Orientation and Dispersion Parameters from a Diffusion Tensor in Healthy White Matter. Front Neurosci 11:720.
Fieremans E, Jensen JH, Helpern JA (2011) White matter characterization with diffusional kurtosis imaging. Neuroimage 58:177188.
Jespersen SN, Olesen JL, Hansen B, Shemesh N (2018) Diffusion time dependence of microstructural parameters in fixed spinal cord. Neuroimage 182:329342.
Polzehl J, Tabelow K (2016) Low SNR in Diffusion MRI Models. Journal of the American Statistical Association, Volume 111, Issue 516: 1480-1490.